Python Tensorflow-zelfstudie

In deze les zullen we kijken naar TensorFlow, een open-source machine learning-bibliotheek die wordt gebruikt voor het ontwerpen, bouwen en trainen van deep learning-modellen. Het is mogelijk numerieke berekeningen uit te voeren met de TensorFlow-bibliotheek, welke gegevensstroomgrafieken waarin wiskundige bewerkingen worden weergegeven als knooppunten en gegevens worden weergegeven als randen tussen die knooppunten.

In het algemeen zullen we in deze les drie hoofdonderwerpen behandelen:

Wat zijn tensoren en TensorFlow?
ML-algoritmen toepassen met TensorFlow
TensorFlow-gebruiksscenario's

TensorFlow is een uitstekend Python-pakket van Google dat goed gebruik maakt van het dataflow-programmeerparadigma voor sterk geoptimaliseerde wiskundige berekeningen. Enkele kenmerken van TensorFlow zijn:

Gedistribueerde rekencapaciteit die het beheren van gegevens in grote sets eenvoudiger maakt
Diep leren en ondersteuning van neurale netwerken is goed
Het beheert complexe wiskundige structuren zoals n-dimensionale arrays zeer efficiënt

Dankzij al deze functies en het scala aan machine learning-algoritmen die TensorFlow implementeert, is het een bibliotheek op productieschaal. Laten we in TensorFlow in concepten duiken, zodat we meteen daarna onze handen vuil kunnen maken met code.

TensorFlow installeren

Aangezien we gebruik gaan maken van Python API voor TensorFlow, is het goed om te weten dat het werkt met zowel Python 2.7 en 3.3+ versies. Laten we de TensorFlow-bibliotheek installeren voordat we naar de daadwerkelijke voorbeelden en concepten gaan. Er zijn twee manieren om dit pakket te installeren:. De eerste omvat het gebruik van de Python-pakketbeheerder, pip:

pip installeren tensorflow

De tweede manier heeft betrekking op Anaconda, we kunnen het pakket installeren als:

conda install -c conda-forge tensorflow

Zoek gerust naar nachtelijke builds en GPU-versies op de officiële installatiepagina's van TensorFlow.

Ik zal de Anaconda-manager gebruiken voor alle voorbeelden in deze les. Ik zal hiervoor een Jupyter Notebook starten:

Nu we klaar zijn met alle importinstructies om wat code te schrijven, laten we beginnen met een duik in het SciPy-pakket met enkele praktische voorbeelden.

Wat zijn tensoren??

Tensoren zijn de basisgegevensstructuren die worden gebruikt in Tensorflow. Ja, ze zijn slechts een manier om gegevens in deep learning weer te geven. Laten we ze hier visualiseren:

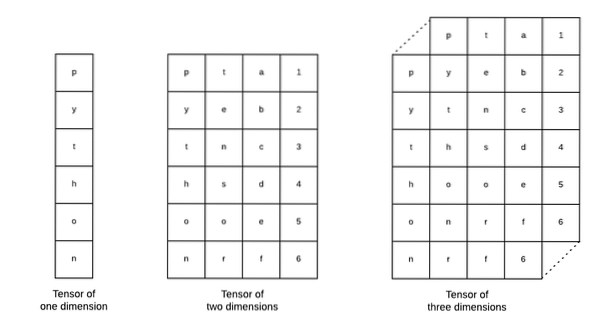
Zoals beschreven in de afbeelding, tensoren kunnen worden aangeduid als n-dimensionale array waarmee we gegevens in complexe dimensies kunnen weergeven. We kunnen elke dimensie zien als een ander kenmerk van gegevens in deep learning. Dit betekent dat Tensors behoorlijk complex kunnen worden als het gaat om complexe datasets met veel functies.

Als we eenmaal weten wat Tensors zijn, denk ik dat het vrij eenvoudig is om af te leiden wat er in TensorFlow gebeurt. Die termen betekenen hoe tensoren of functies in datasets kunnen stromen om waardevolle output te produceren terwijl we er verschillende bewerkingen op uitvoeren.

TensorFlow begrijpen met constanten

Zoals we hierboven lezen, stelt TensorFlow ons in staat om machine learning-algoritmen op Tensors uit te voeren om waardevolle output te produceren. Met TensorFlow is het ontwerpen en trainen van Deep Learning-modellen eenvoudig.

TensorFlow wordt geleverd met bouwen Berekeningsgrafieken. Berekeningsgrafieken zijn de gegevensstroomgrafieken waarin wiskundige bewerkingen worden weergegeven als knooppunten en gegevens worden weergegeven als randen tussen die knooppunten. Laten we een heel eenvoudig codefragment schrijven om een concrete visualisatie te geven:

importeer tensorflow als tf
x = tf.constante (5)
y = tf.constante (6)
z = x * y
print(z)

Wanneer we dit voorbeeld uitvoeren, zien we de volgende uitvoer:

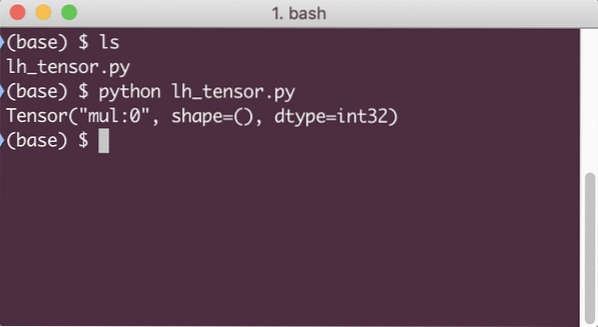
Waarom is de vermenigvuldiging verkeerd?? Dat hadden we niet verwacht. Dit is gebeurd omdat dit niet is hoe we bewerkingen kunnen uitvoeren met TensorFlow. Eerst moeten we beginnen met een sessie om de rekengrafiek werkend te krijgen,

Met Sessions kunnen we inkapselen de controle van de operaties en de toestand van Tensors. Dit betekent dat een sessie ook het resultaat van een berekeningsgrafiek kan opslaan, zodat het dat resultaat kan doorgeven aan de volgende bewerking in de volgorde van uitvoering van de pijplijnen. Laten we nu een sessie maken om het juiste resultaat te krijgen:

# Begin met het sessie-object
sessie = tf.Sessie()
# Geef de berekening aan de sessie en sla deze op
resultaat = sessie.rennen(z)
# Druk het resultaat van de berekening af
afdrukken (resultaat)
# Sluit sessie
sessie.dichtbij()

Deze keer hebben we de sessie verkregen en deze voorzien van de berekening die nodig is om op de knooppunten te draaien. Wanneer we dit voorbeeld uitvoeren, zien we de volgende uitvoer:

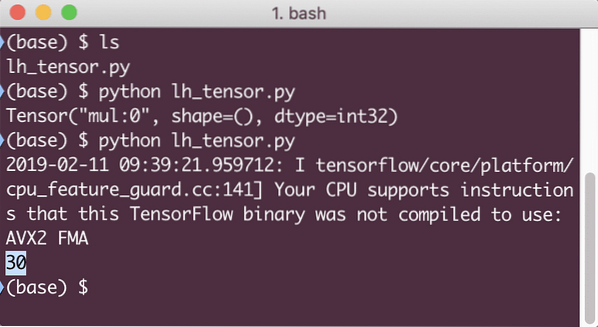
Hoewel we een waarschuwing van TensorFlow hebben ontvangen, hebben we nog steeds de juiste uitvoer van de berekening.

Tensorbewerkingen met één element

Net zoals we in het laatste voorbeeld twee constante Tensors hebben vermenigvuldigd, hebben we veel andere bewerkingen in TensorFlow die op afzonderlijke elementen kunnen worden uitgevoerd:

toevoegen
aftrekken
vermenigvuldigen
div
mod
buikspieren
negatief
teken
plein
ronde
sqrt
pow
exp
log
maximum
minimum
omdat
zonde

Bewerkingen met één element betekent dat zelfs wanneer u een array opgeeft, de bewerkingen worden uitgevoerd op elk van de elementen van die array. Bijvoorbeeld:

importeer tensorflow als tf
importeer numpy als np
tensor = np.reeks([2, 5, 8])
tensor = tf.convert_to_tensor(tensor, dtype=tf.zweven64)
met tf.Session() als sessie:
print(sessie).rennen (tf.cos(tensor)))

Wanneer we dit voorbeeld uitvoeren, zien we de volgende uitvoer:

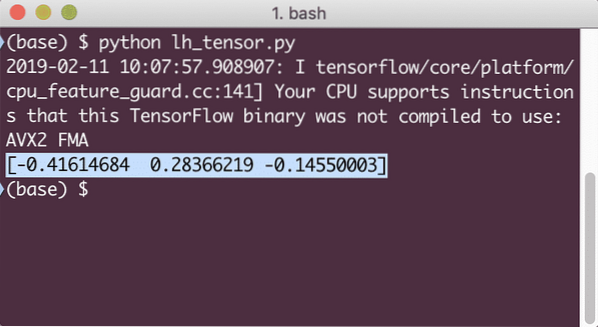
We begrepen hier twee belangrijke concepten:

Elke NumPy-array kan eenvoudig worden omgezet in een Tensor met behulp van de functie convert_to_tensor
De bewerking is uitgevoerd op elk van de NumPy-array-elementen

Tijdelijke aanduidingen en variabelen

In een van de vorige paragrafen hebben we gekeken hoe we Tensorflow-constanten kunnen gebruiken om rekengrafieken te maken. Maar TensorFlow stelt ons ook in staat om input te nemen op de vlucht, zodat de berekeningsgrafiek dynamisch van aard kan zijn. Dit is mogelijk met behulp van Placeholders en Variables.

In werkelijkheid bevatten tijdelijke aanduidingen geen gegevens en moeten ze geldige invoer krijgen tijdens runtime en zoals verwacht, zonder invoer, zullen ze een fout genereren.

Een tijdelijke aanduiding kan worden aangeduid als een overeenkomst in een grafiek dat een invoer tijdens runtime zeker zal worden verstrekt. Hier is een voorbeeld van plaatsaanduidingen:

importeer tensorflow als tf
# Twee tijdelijke aanduidingen
x = tf. tijdelijke aanduiding (tf.vlotter32)
y = tf. tijdelijke aanduiding (tf.vlotter32)
# Vermenigvuldiging toewijzen w.r.t. een & b naar knooppunt mul
z = x * y
# Creëer een sessie
sessie = tf.Sessie()
# Waarden doorgeven voor tijdelijke aanduidingen
resultaat = sessie.uitvoeren(z, x: [2, 5], y: [3, 7])
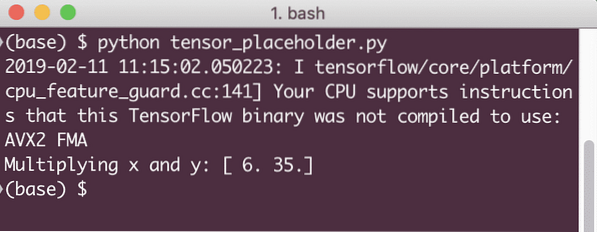
print('X en y vermenigvuldigen:', resultaat)

Wanneer we dit voorbeeld uitvoeren, zien we de volgende uitvoer:

Nu we kennis hebben over tijdelijke aanduidingen, gaan we ons richten op variabelen. We weten dat de uitvoer van een vergelijking in de loop van de tijd kan veranderen voor dezelfde set invoer. Dus als we onze modelvariabele trainen, kan het zijn gedrag in de loop van de tijd veranderen. In dit scenario stelt een variabele ons in staat om deze trainbare parameters toe te voegen aan onze rekengrafiek. Een variabele kan als volgt worden gedefinieerd:

x = tf.Variabele( [5.2], dtype = tf.vlotter32 )

In de bovenstaande vergelijking is x een variabele waarvan de initiële waarde en het gegevenstype wordt gegeven. Als we het datatype niet verstrekken, wordt het afgeleid door TensorFlow met zijn initiële waarde. Raadpleeg hier de gegevenstypen van TensorFlow:.

In tegenstelling tot een constante, moeten we een Python-functie aanroepen om alle variabelen van een grafiek te initialiseren:

init = tf.global_variables_initializer()
sessie.uitvoeren (init)

Zorg ervoor dat u de bovenstaande TensorFlow-functie uitvoert voordat we onze grafiek gebruiken.

Lineaire regressie met TensorFlow

Lineaire regressie is een van de meest voorkomende algoritmen die worden gebruikt om een relatie tot stand te brengen in bepaalde continue gegevens. Deze relatie tussen de coördinaatpunten, zeg x en y, wordt a . genoemd hypothese. Als we het hebben over lineaire regressie, is de hypothese een rechte lijn:

y = mx + c

Hier is m de helling van de lijn en hier is het een vector die voorstelt gewichten. c is de constante coëfficiënt (y-snijpunt) en hier vertegenwoordigt het de Vooroordeel. Het gewicht en de bias worden de . genoemd parameters van het model.

Lineaire regressies stellen ons in staat om de waarden van gewicht en bias zo te schatten dat we een minimum hebben kostenfunctie. Ten slotte is de x de onafhankelijke variabele in de vergelijking en is y de afhankelijke variabele. Laten we nu beginnen met het bouwen van het lineaire model in TensorFlow met een eenvoudig codefragment dat we zullen uitleggen:

importeer tensorflow als tf
# Variabelen voor parameter helling (W) met initiële waarde als 1.1
W = tf.Variabele([1.1], tf.vlotter32)
# Variabele voor bias (b) met initiële waarde als -1.1
b = tf.Variabele([-1.1], tf.vlotter32)
# Tijdelijke aanduidingen voor het verstrekken van invoer of onafhankelijke variabele, aangegeven met x
x = tf.tijdelijke aanduiding (tf.vlotter32)
# Vergelijking van lijn of de lineaire regressie
lineair_model = W * x + b
# Alle variabelen initialiseren variable
sessie = tf.Sessie()
init = tf.global_variables_initializer()
sessie.uitvoeren (init)
# Regressiemodel uitvoeren
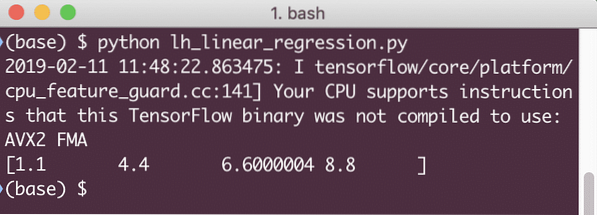
print(sessie).uitvoeren(lineair_model x: [2, 5, 7, 9]))

Hier hebben we precies gedaan wat we eerder hebben uitgelegd, laten we het hier samenvatten:

We zijn begonnen met het importeren van TensorFlow in ons script
Maak enkele variabelen om het vectorgewicht en de parameterbias weer te geven
Er is een tijdelijke aanduiding nodig om de invoer weer te geven, x
Vertegenwoordig het lineaire model
Initialiseer alle waarden die nodig zijn voor het model

Wanneer we dit voorbeeld uitvoeren, zien we de volgende uitvoer:

Het eenvoudige codefragment geeft slechts een basisidee over hoe we een regressiemodel kunnen bouwen. Maar we moeten nog enkele stappen uitvoeren om het model dat we hebben gebouwd te voltooien:

We moeten ons model zelf-trainbaar maken, zodat het output kan produceren voor elke gegeven input
We moeten de output van het model valideren door deze te vergelijken met de verwachte output voor gegeven x

Verliesfunctie en modelvalidatie

Om het model te valideren, moeten we een meting hebben van hoe de huidige output is afgeweken van de verwachte output. Er zijn verschillende verliesfuncties die hier voor validatie kunnen worden gebruikt, maar we zullen een van de meest voorkomende methoden bekijken:, Som van gekwadrateerde fout of SSE.

De vergelijking voor SSE wordt gegeven als:

E = 1/2 * (t - y)2

Hier:

E = gemiddelde kwadratische fout
t = Ontvangen uitgang
y = Verwachte output
t - y = Fout

Laten we nu een codefragment schrijven in het verlengde van het laatste fragment om de verlieswaarde weer te geven:

y = tf.tijdelijke aanduiding (tf.vlotter32)
error = lineair_model - y
squared_errors = tf.vierkant (fout)
verlies = tf.reduce_sum(squared_errors)
print(sessie).run(verlies, x:[2, 5, 7, 9], y:[2, 4, 6, 8]))

Wanneer we dit voorbeeld uitvoeren, zien we de volgende uitvoer:

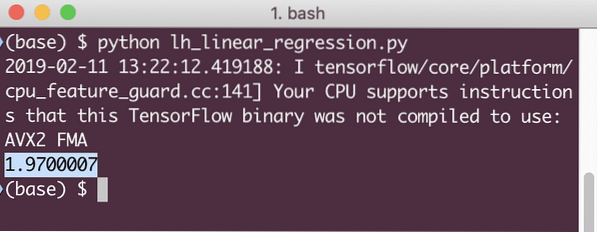
Het is duidelijk dat de verlieswaarde erg laag is voor het gegeven lineaire regressiemodel.

Conclusie

In deze les hebben we gekeken naar een van de meest populaire deep learning- en machine learning-pakketten, TensorFlow. We hebben ook een lineair regressiemodel gemaakt met een zeer hoge nauwkeurigheid.